- Details
For subwoofers, the acoustic center might be located — outside the enclosure — about one foot in front the loudspeaker.
"The acoustic center represents the point from which
the far‑field waves emanate — including their phase —
when projected back to the source."
— John Vanderkooy —
BEng, PhD (McMaster) – Distinguished Professor Emeritus
Audio Research Group, University of Waterloo (CA)
This point, acoustically, seems to — act — as the center of the loudspeaker at lower frequencies. The locus of an equivalent point source that yields the same far‑field
pressure in magnitude and phase. And when left unaccounted for, prevents one from reconciling field measurements and listening tests with theory and prediction methods.
- Details
This is a cautionary tale about the risk of drawing wrong conclusions when being unable to — self‑check — one's own data interpretation. Whereby turning analyzer usage into a video game. And treating the on‑screen data as gospel with blind faith. To paraphrase Jamie Anderson:
"Calling it (the hardware and/or software) analyzer is a misnomer,
the operator is the analyzer."
— Jamie Anderson —
President and founding member of Rational Acoustics
- Details
White noise is a random signal having equal intensity at all frequencies. And refers to a — statistical model — for signals, as opposed to any specific signal. In discrete time, white noise is a signal whose samples are regarded as a sequence of — serially uncorrelated — random variables with zero mean and finite variance. Where — any — zero‑mean distribution of values (without DC component) is possible.
- Details
This article explores reasons for considering frequency shading — as opposed to gain shading — to optimize the tonal uniformity of line arrays.
"I envy people that spend their carreers in studios or post‑production facilities.
Because there will never be enough air between them and their studio monitors
for air absorption to become a problem."
— Merlijn van Veen —
- Details
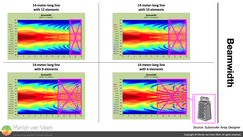Figure 1This may come as a shock — coming from the author of the Subwoofer Array Designer — but over the years I have grown an increasing dislike for horizontal subwoofer arrays.
The only thing they really have got going for them, is their left‑to‑right spatial uniformity — provided — they do not fall victim to one honest mistake.